February 27, 2022
Score and Win Predictor
After earning my cricket analytics certificate, I started applying some of the techniques I learned to analyze data from both the South Africa vs. India Test series and the Ashes in 2021/22. Through this experience, I was able to take a closer look at very intriguing aspects of the game such as a team’s reliance on a single batter, batters that have stepped up when their team is under pressure, effectiveness of teams with the ball based on how old it is, and so on.
Once I got a taste of data analytics in cricket thanks to the above experiments, I wanted to build something bigger. Drawing inspiration from popular prediction tools used in the industry such as ESPNcricinfo’s Forecaster and CricViz’s WinViz, I felt it would be cool to apply the AI & ML knowledge that I gained at university level to solve this problem on my own.
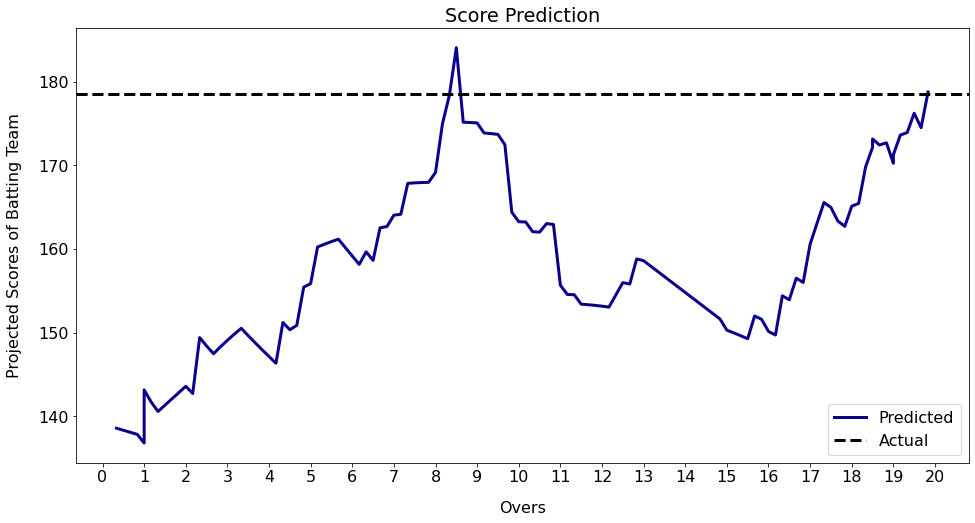
Sri Lanka batting first vs. India - 2nd T20I - 2022
The above plot shows Sri Lanka’s projected scores using a linear regression model at different stages. It considers the current run rate, number of balls left, and number of wickets in hand to predict the run rate for the remainder of the innings which is then used to calculate the expected final score.
Ball-by-ball data from 800+ T20 international matches provided by Cricsheet is used for this experiment such that 80% of the data is used for training and the remaining 20% is used for testing.
model_data = pd.read_csv('batting_first_data.csv')
X = model_data.iloc[:, :-1]
y = model_data.iloc[:, -1]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42)
Before training though, a pipeline is constructed through which the features are first standardized and then passed to the model.
reg = LinearRegression()
pipe = make_pipeline(StandardScaler(), reg)
pipe.fit(X_train, y_train)
y_pred_lr = pipe.predict(X_test)
After making predictions on the test set using the trained model, 3 things are used to evaluate it: adjusted R-squared, RMSE/MAE, and a residual plot. The adjusted R-squared value observed for this experiment is 0.1742 which appears to be really low and might give the impression that the chosen model is not good. That, however, isn’t necessarily the case.
def adj_r2_score(r2_score, n, k):
return 1 - (1 - r2_score) * (n - 1) / (n - k - 1)
r2_score = metrics.r2_score(y_test, y_pred_lr)
n, k = X_test.shape
print('R² = %.4f' % r2_score)
print('adj. R² = %.4f' % adj_r2_score(r2_score, n, k))
RMSE and MAE are 2 error measures that are often used in statistics which give us the average difference between the observed and the predicted values. My regression model had an RMSE of 2.9126 and an MAE of 2.0598 which suggests that, on average, there is a difference of just 2-3 runs per over between what the model predicts and what run rate the batting team actually achieves.
print('RMSE = %.4f' % np.sqrt(metrics.mean_squared_error(y_test, y_pred_lr)))
print('MAE = %.4f' % metrics.mean_absolute_error(y_test, y_pred_lr))
Lastly, the predicted values are plotted against the standardized residuals. This seems to meet most of the requirements but there probably is some room for improvement. More importantly, it shows that the prediction error is consistent for a significantly large number of points even though the adjusted R-squared value is low. This tells us that the model might be adequate for the given problem.
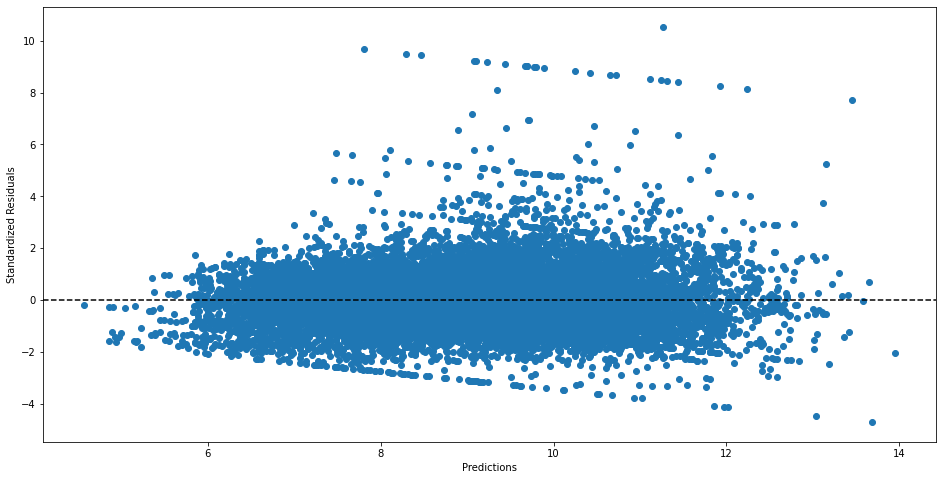
Residual plot for the linear regression model
Predicting the final score for the team batting first is only one half of the experiment though. The next task is to use ball-by-ball data from T20I chases to build a win prediction model using logistic regression.
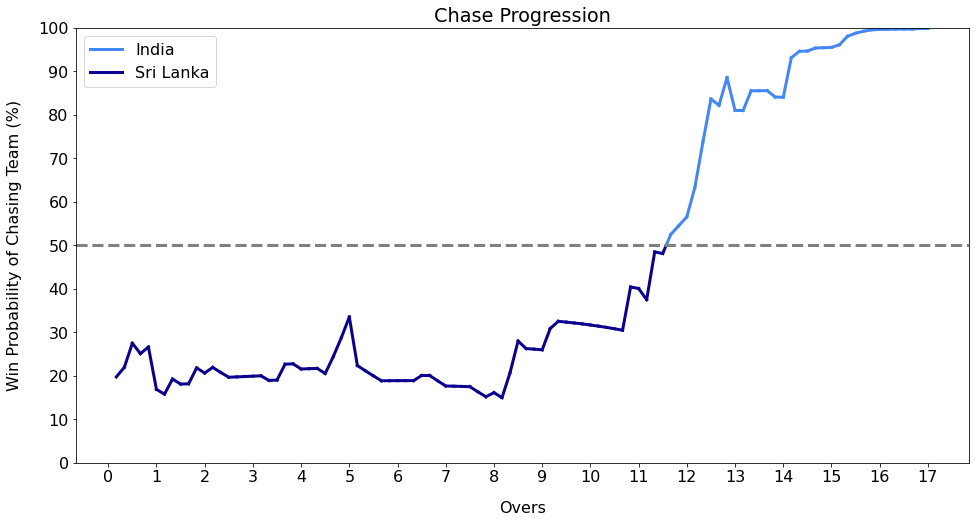
India chasing vs. Sri Lanka - 2nd T20I - 2022
Note that in the above plot, the value that the line corresponds to only represents the chasing team’s win probability but the color indicates which team is ahead in the game at any given point in time.
A lot of the steps involved in this are very similar to the score predictor but additionally other key features such as the target to be chased, runs remaining, and required run rate are also included. The evaluation procedure is different as well - classification report, ROC AUC, and confusion matrix are used instead and the last 2 of those are as shown below.
metrics.RocCurveDisplay.from_predictions(y_test, y_pred)
metrics.ConfusionMatrixDisplay.from_predictions(y_test, y_pred, normalize = 'true', cmap = plt.cm.Blues)
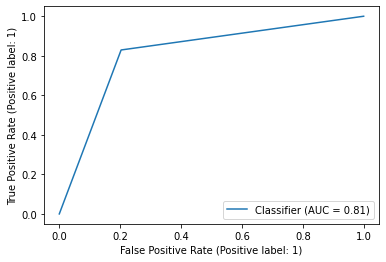
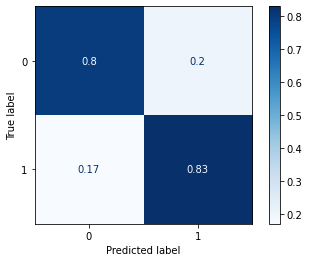
ROC AUC and confusion matrix for the logistic regression model
Both the prediction models seem to perform well not only based on the evaluation metrics but also based on how well the graphs capture the different events that happen during live games, i.e., there is a clear connection between the direction of the line and an event in the game such as a six, four, dot ball, or wicket.
Outputs produced by non-linear models such as decision trees and random forests appear to lack this connection despite producing similar performance levels. For example, a wicket falling might hardly lead to any change in the line’s direction and then an over later, it might drop sharply for no apparent reason. This isn’t very intuitive and may seem confusing from a viewer’s perspective. Tuning the hyperparameters of these models could potentially help mitigate this issue.
Considering other features such as which batsmen are at the crease, the quality of opposition bowlers, how good specific players are in certain phases of play, the ground/pitch/weather conditions, etc. may also help in building superior models. Acquiring all this information for past matches and then using it for model training, however, can be quite challenging.
The full code for the 2 models discussed above can be found here.