August 29, 2022
Meta-Learning for Full Match Prediction
In an earlier post, we attempted to predict the batting team’s score in the first innings and the chasing team’s win probability in the second. Thereafter, in another post, we tried to classify sequences of fixed length using LSTMs.
The objective in this post is to combine these ideas to some extent by building an LSTM that can be used to predict both the score and the win probability right from the start of each match by learning to handle sequences of variable length. Additionally, it is compared with linear approaches and to further boost performance, a stacking-based ensemble is implemented.
While testing the previous predictor during this year’s IPL, I noticed that it would always generate the same output in all games for a given situation. For example, 120/3 after 15 overs or 50 to win from 30 balls with 5 wickets left would produce the exact same result every single time.
This did not feel right since it does not take the sequence of events that lead to that situation into consideration. It is for that purpose that a recurrent neural network architecture is adopted in order to capture any “momentum shifts” throughout the match and build something similar to “Match Reel” by Cricket.com.
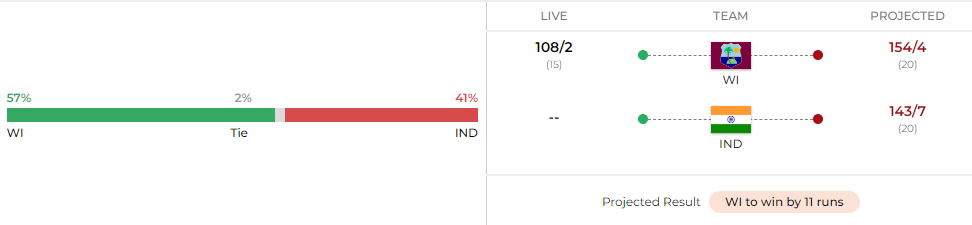
Match Reel (source: Cricket.com)
The same data source as before is used for this project but in a slightly different format. Instead of using separate files for each innings, all of the necessary information is available in a single file with a -1 set for any fields that are not applicable at any point. This value can also be modified with a simple update, if required.
mask_value = -1
data.replace(-1, mask_value, inplace = True)
Each match has a different number of samples because of some innings ending earlier than others or due to extras. An LSTM cannot handle such sequences directly and so, one has to transform each sequence to be of fixed length. This can be done by padding and masking - dummy values are appended at the end but are ignored during training.
max_time_steps = data.groupby('match_id').apply(lambda x: x.shape[0]).max()
def pad_rows(match):
time_steps = match.shape[0]
diff = max_time_steps - time_steps
mask = [mask_value] * (data.shape[1] - 2)
mask.append(match.winner.iloc[0])
mask.append(0)
padding = pd.DataFrame([mask] * diff, columns = data.columns)
return pd.concat([match, padding], ignore_index = True)
data = data.groupby('match_id', sort = False).apply(pad_rows).reset_index(drop = True)
The functional API in Keras is used to define the model’s topology since there are two output units at the end that both depend on the same LSTM layer. This not only provides greater flexibility but also helps in creating a model that can potentially learn the relationship between outputs in addition to the input-output mapping.
The return_sequences parameter of the LSTM layer is set to true since it needs to be trained on every single time step and not just for the match as a whole. Multiple such LSTM layers can be stacked in build_lstm() by passing a higher value for the num_lstm parameter, if needed.
def build_lstm(memory_units = 32, num_lstm = 1, train = True, learning_rate = 1e-3, num_epochs = 150, batch_size = 32, patience = 5):
...
...
inputs = Input(shape = (max_time_steps, input_features.shape[1]))
x = Masking(mask_value = mask_value)(inputs)
lstm = LSTM(memory_units, return_sequences = True)(x)
for i in range(num_lstm - 1):
lstm = LSTM(memory_units, return_sequences = True)(lstm)
output1 = Dense(1, activation = 'sigmoid', name = 'winner')(lstm)
output2 = Dense(1, name = 'score')(lstm)
model = Model(inputs, [output1, output2])
model.compile(
loss = {
'winner': 'binary_crossentropy',
'score': rmse
},
optimizer = tf.keras.optimizers.Adam(learning_rate = learning_rate)
)
...
...
Keras, by default, provides ‘mse’ and ‘mae’ regression losses but does not provide one for ‘rmse’. It does, however, support the use of custom losses as long as they have the signature loss_fn(y_true, y_pred). The following accomplishes this and it is important to note that using K.abs() here helps eliminate the possibility of “nan” being returned while training.
def rmse(y_true, y_pred):
return K.abs(K.sqrt(tf.keras.losses.MSE(y_true, y_pred)))
Once all this is set up, the model can be trained. After several experiments, 64 memory units, a batch size of 128, and an early stopping patience value of 10 epochs are found to produce the best results. All other parameters retain their default values and remain unchanged.
The loss curves suggest that the LSTM is able to generalize well for both tasks and hence, it is also expected to do well in practice. Predictions are made on the validation and test sets to gather more evidence and justify that this is indeed the case.
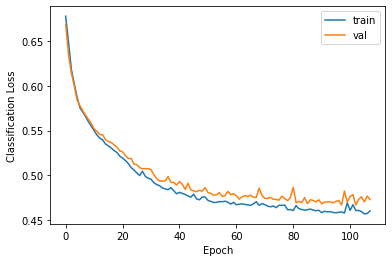
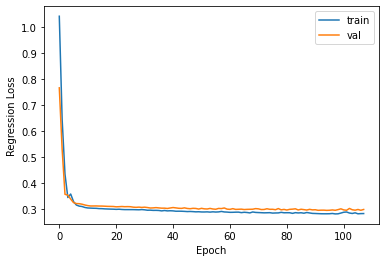
Loss plots - LSTM model
In order to gauge the performance levels of the LSTM even better, the average prediction error over time is compared to that of the linear models for each task. In the classification case, it outperforms logistic regression most of the time, barring a phase in the last 6-7 overs where the latter is clearly the superior one.
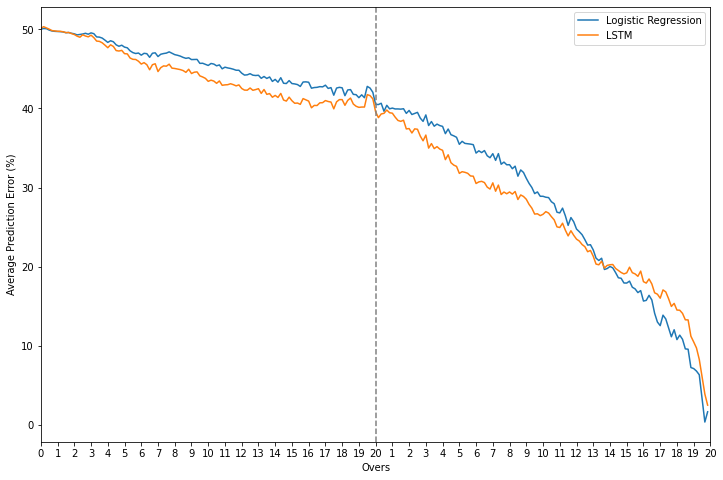
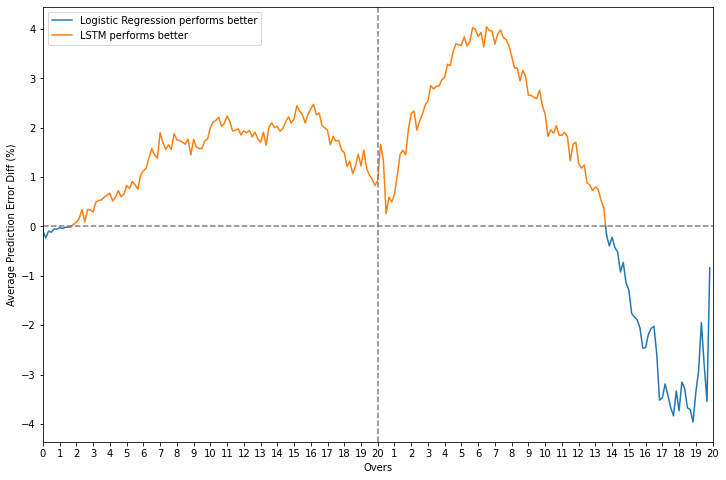
Error and error difference plots - LSTM vs. logistic regression
For the regression task, linear regression outperforms the LSTM in most cases but the error difference between the two is mostly between just +0.5 to -0.5 while attempting to predict the team’s final score. There is, however, an evident spike at the beginning of the second innings which shows that the LSTM’s prediction is, on average, 2 runs more accurate than that of linear regression when the chase starts.
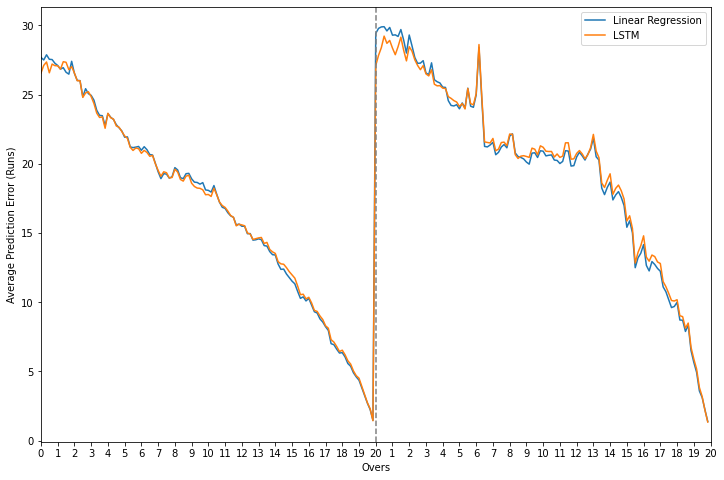
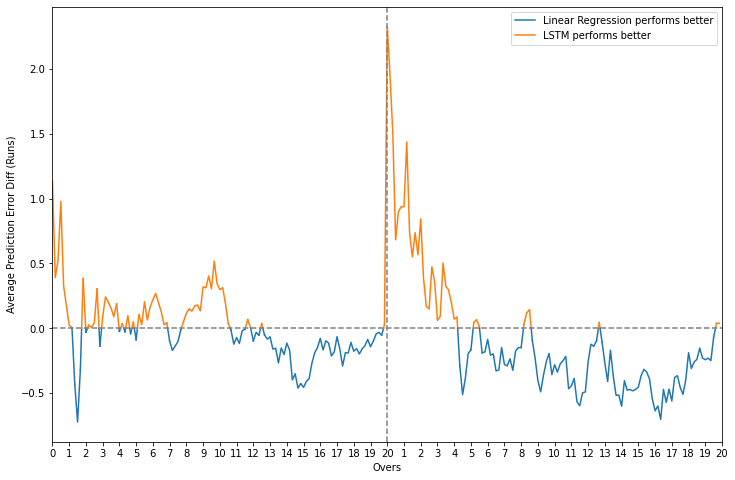
Error and error difference plots - LSTM vs. linear regression
Looking at how different models perform better depending on the phase of the game, it makes sense to combine them in some way so that the output of the “best” one is given more importance at every stage. This can be accomplished by stacking them together.
Specifically, for each task, another model (meta-learner) is created which learns how to best combine the predictions from the individual models (base learners). In summary, the whole process works as follows: train the base learners on the training set, make predictions on the validation set, train the meta-learners on the validation set which includes the base learner predictions, and finally, evaluate on the test set.
While there is no distinguishable increase in performance for the regression task, it is clear that while predicting the win probability, the meta-model is able to identify the points at which it needs to shift its focus from one base model to the other.
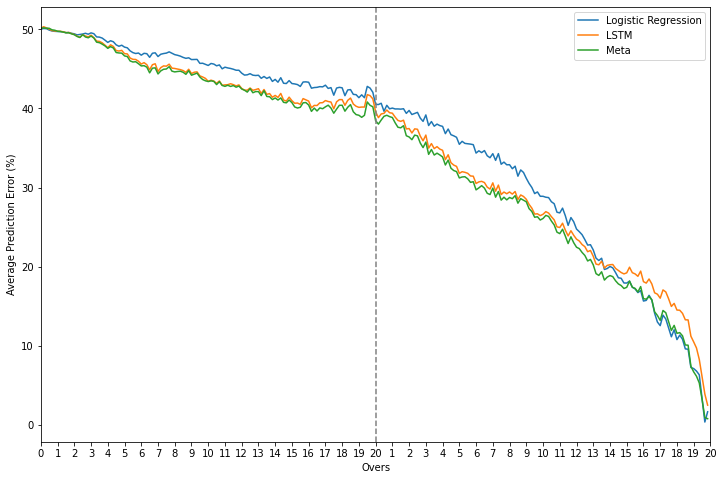
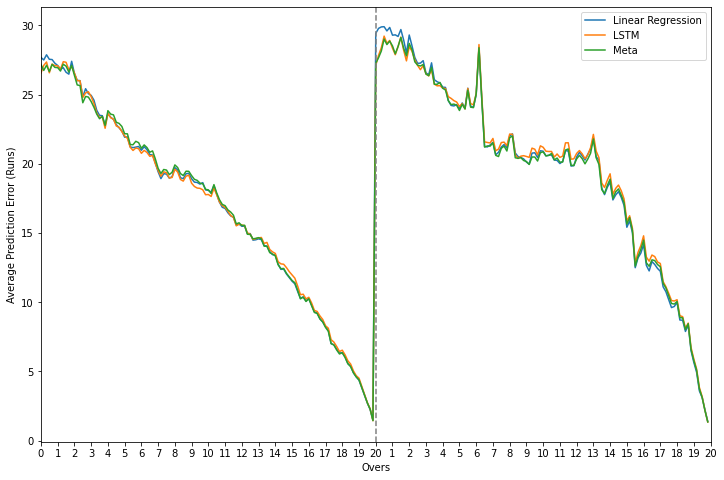
Error plots - meta-learners vs. base learners for both tasks
On closer inspection, it can be seen that the meta-model almost always outperforms the base models across all phases of a game while predicting the win probability. There is still a little phase in the last 5 overs where logistic regression is the best option but the difference in error has been considerably reduced from up to 4% vs. LSTM to less than 1%.
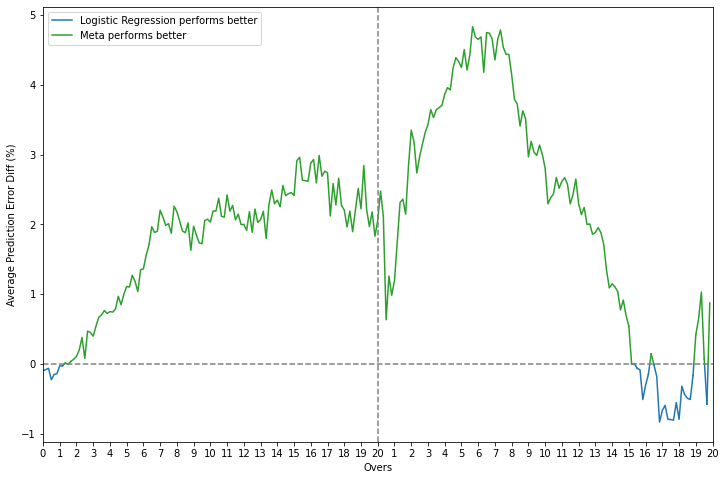
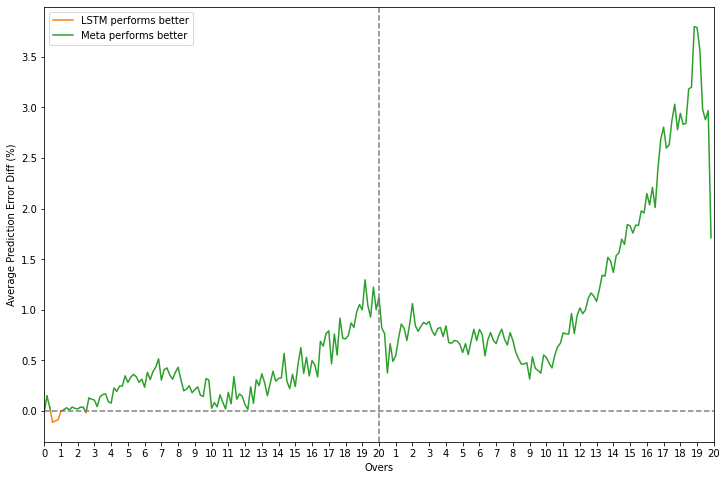
Error difference plots - meta-learner vs. base learners for classification
As mentioned previously, the three models perform very similary while predicting the score and there is no obvious winner to choose from. The meta-model, however, has a lower error than the LSTM for most of the chase and a comparatively lower error difference vs. linear regression. For the sake of consistency as well, it remains the preferred option but there is no harm in picking one of the base models either.
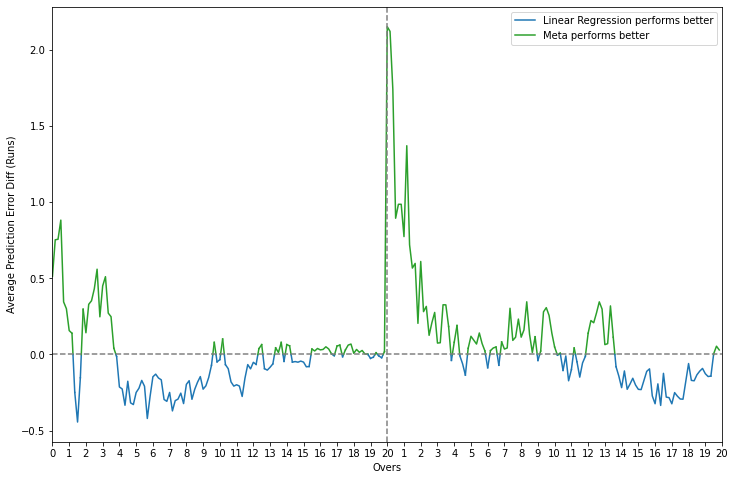
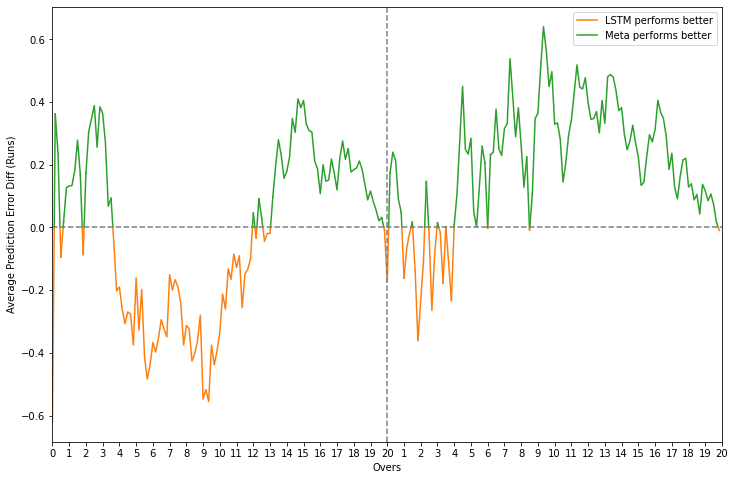
Error difference plots - meta-learner vs. base learners for regression
The final base models are trained on all the available data and are used to make predictions on the entire dataset. The final meta-learners are then fit on this data and are ready to be used in a live game. The animated version of one such real-world example is shown below.
Each plot is generated using matplotlib’s FuncAnimation class and can be time-consuming to run on a local machine. An alternative is to make a few changes and run them like regular plotting functions to quickly produce static graphs instead.
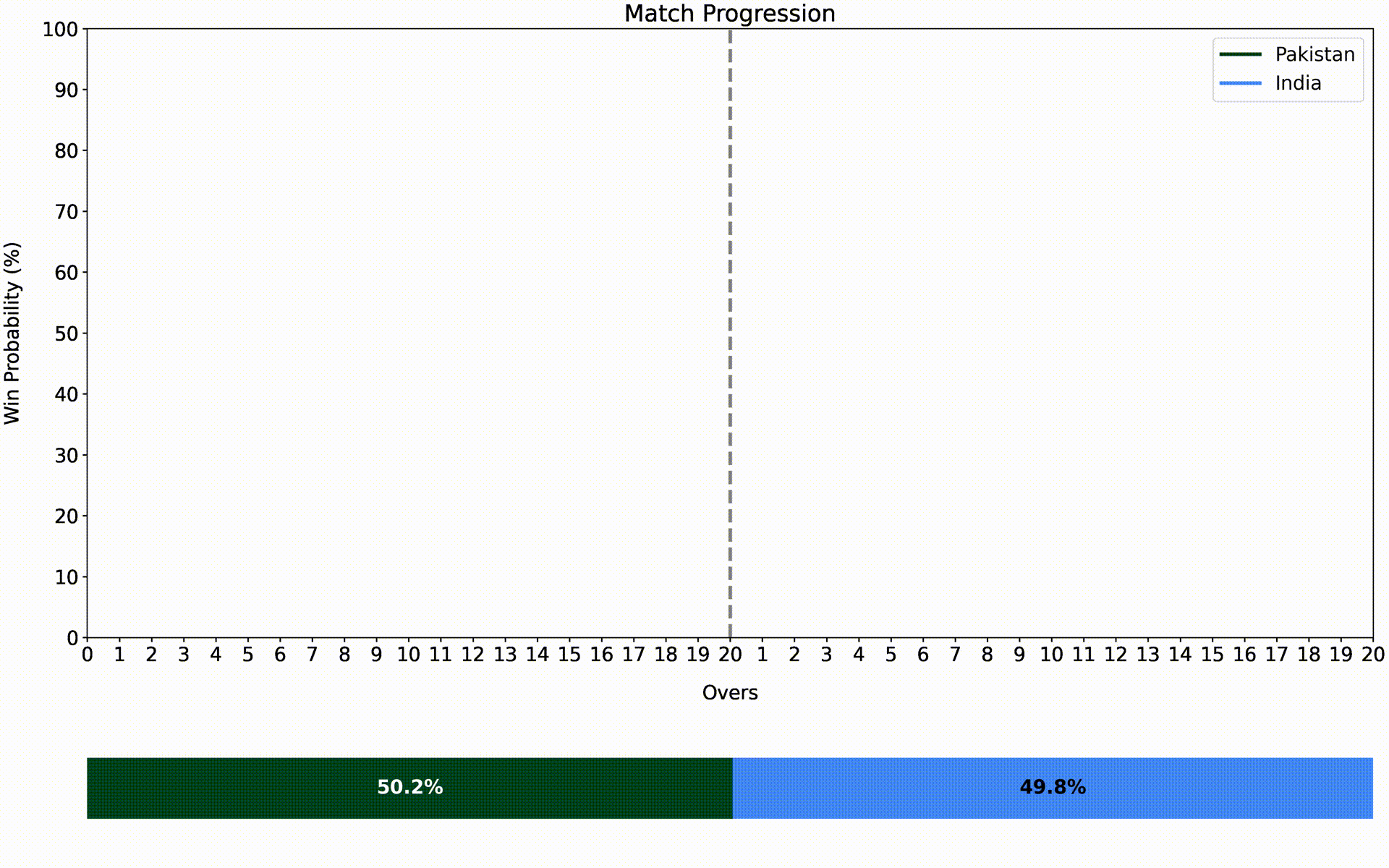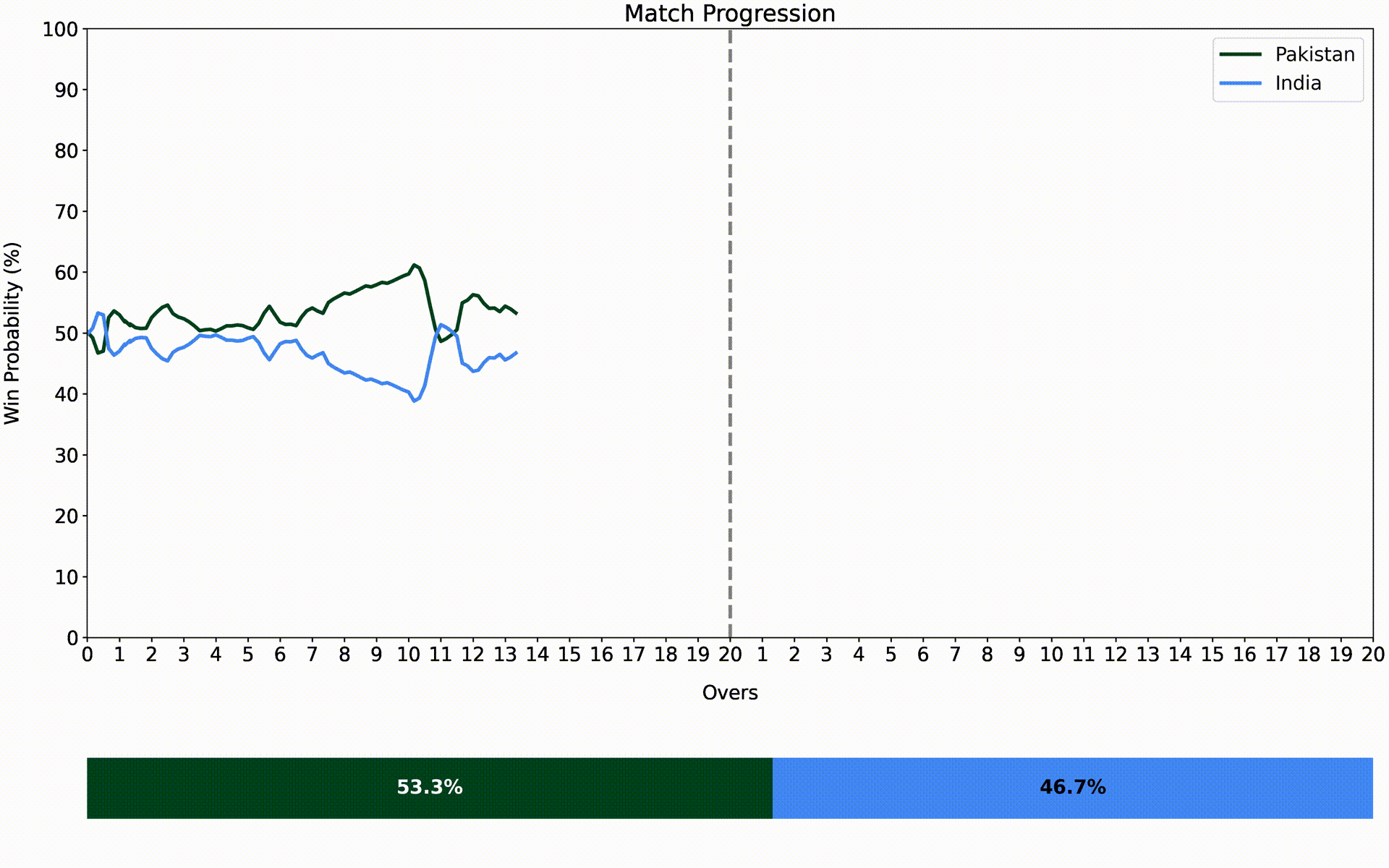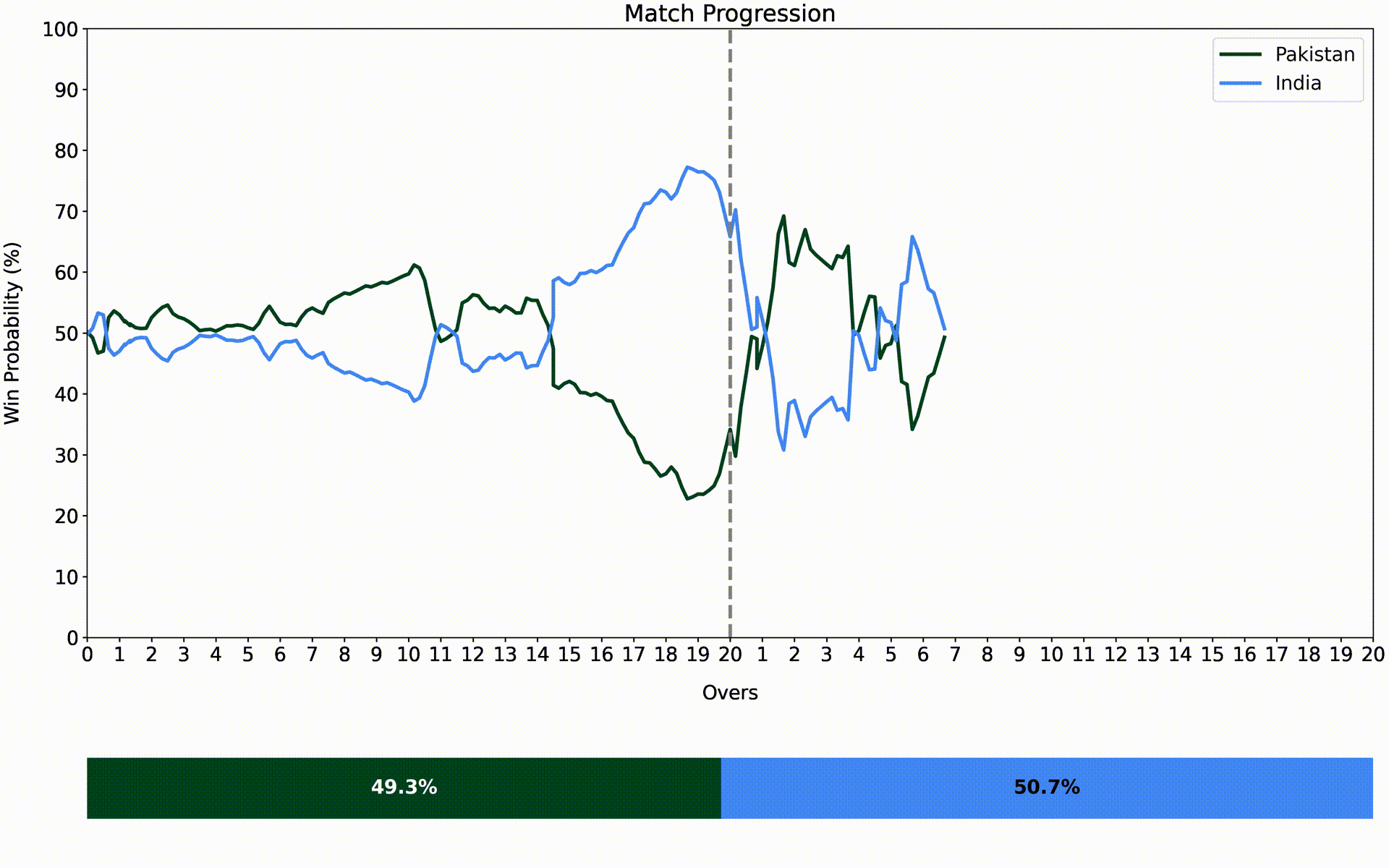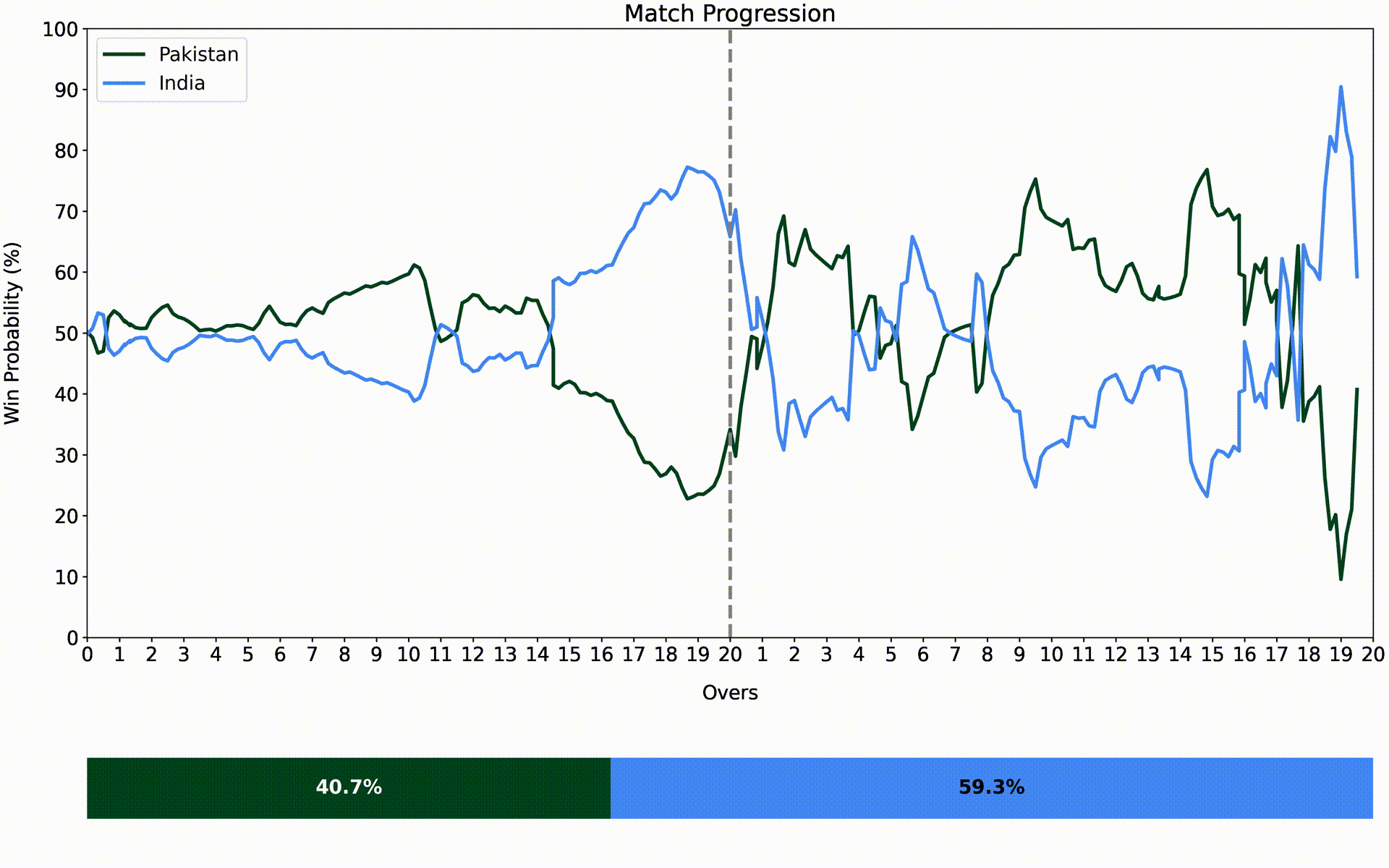
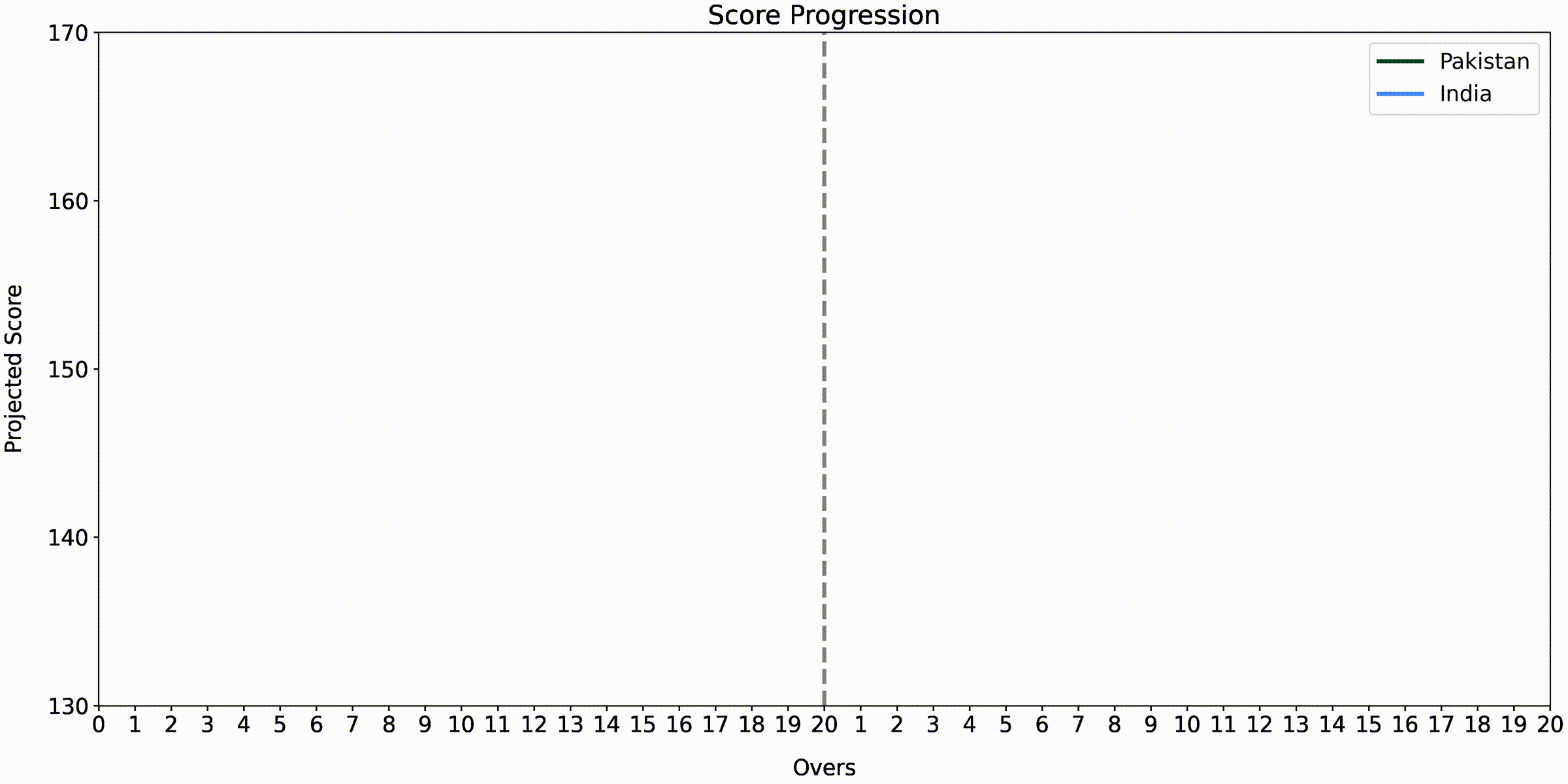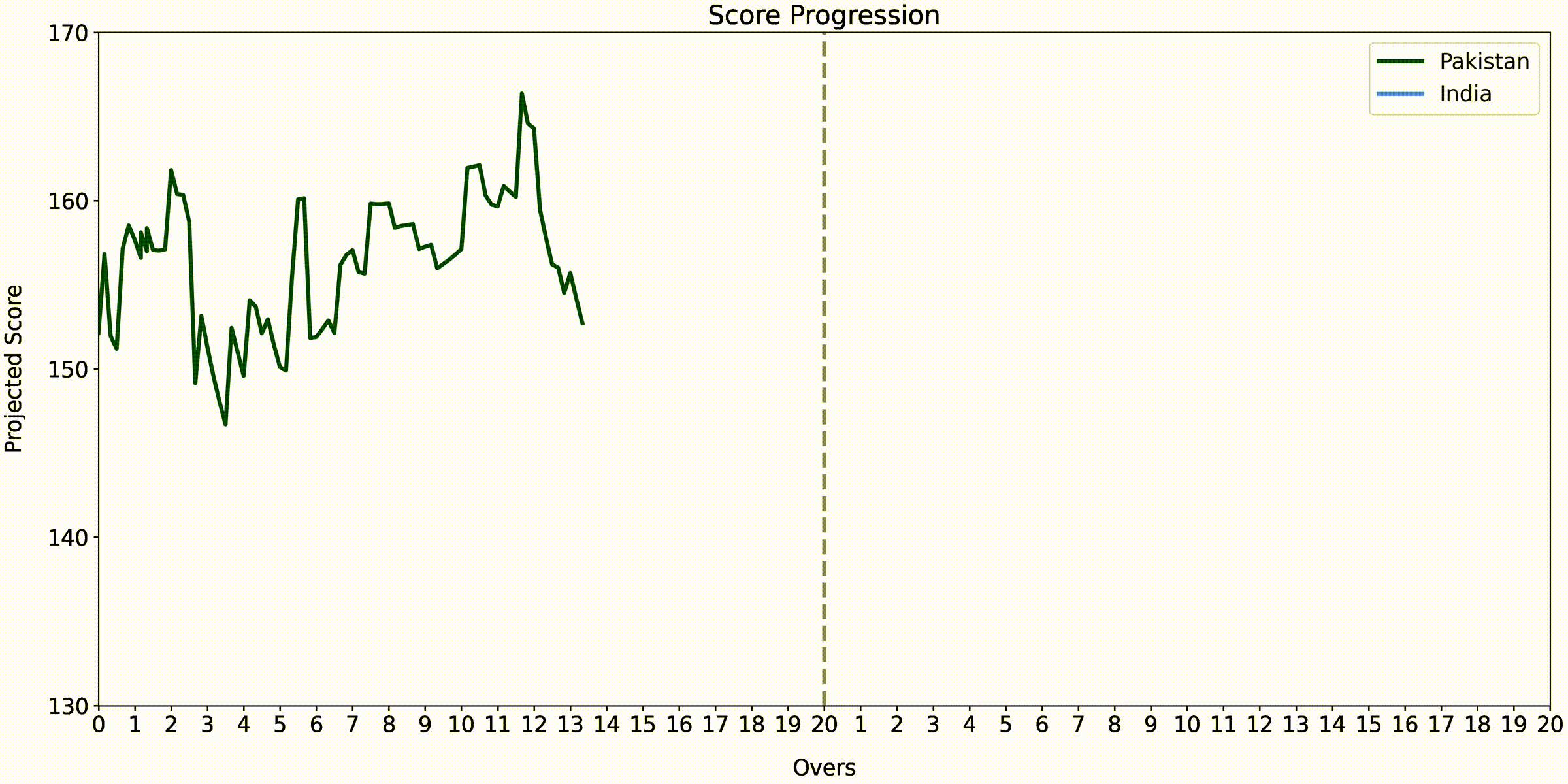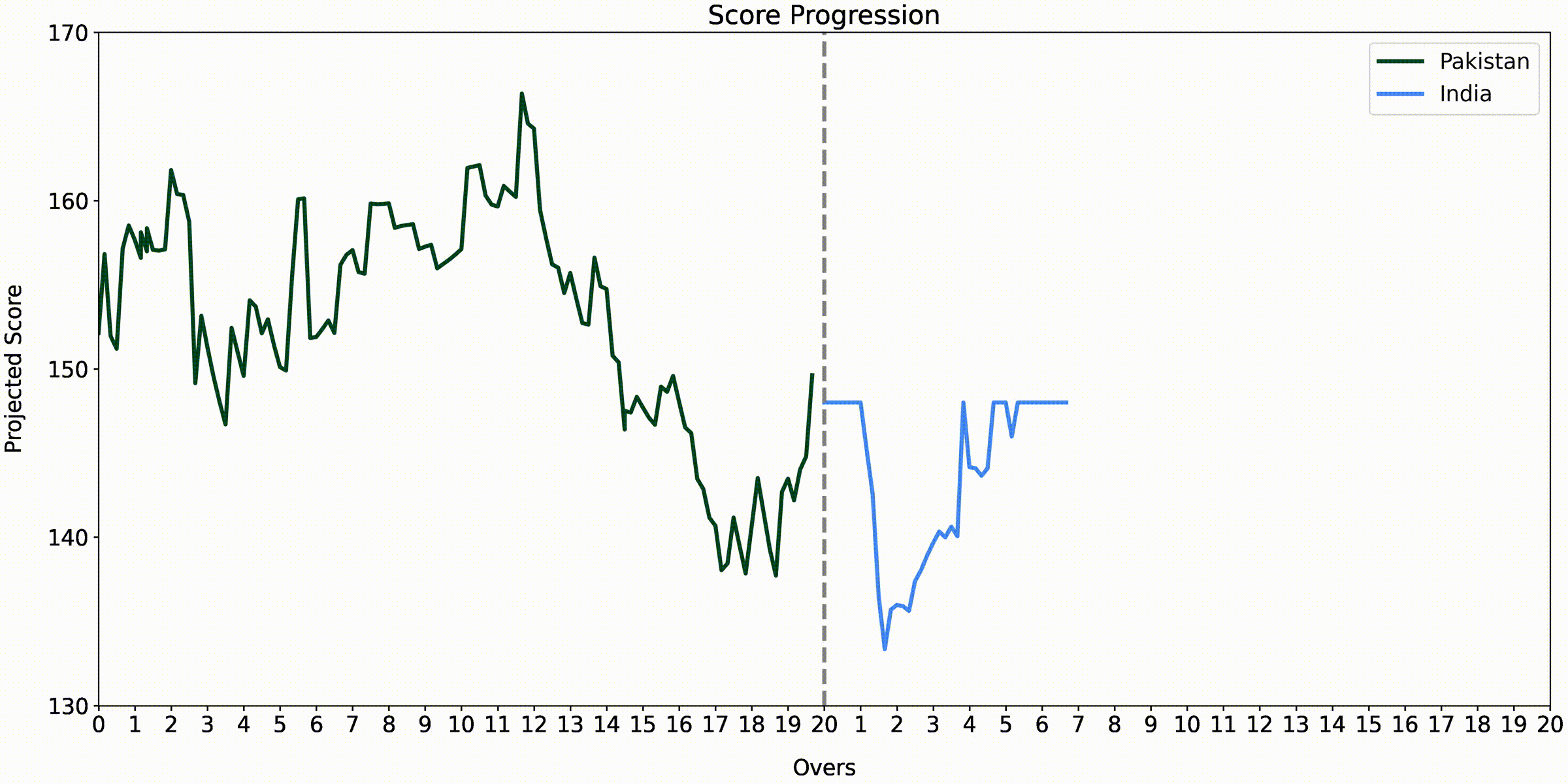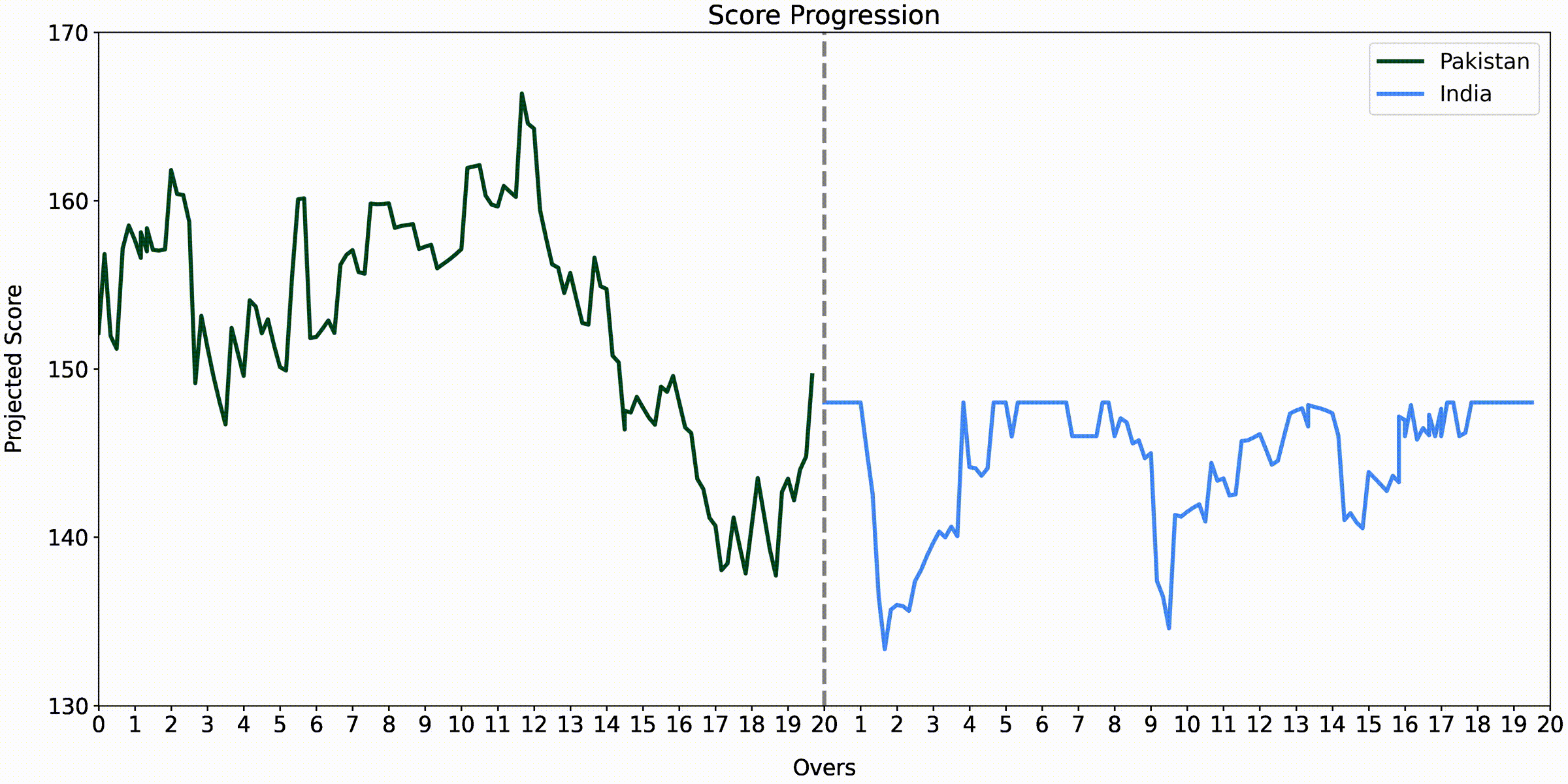
India vs. Pakistan - Asia Cup 2022
While this is very similar to Match Reel, there are two ways in which it could potentially be improved further. In the first innings, Cricket.com not only predicts the batting team’s final score but also the chasing team’s at every point. Secondly, the expected number of wickets to fall is also predicted for both. These may not be that important since it is hard to estimate them accurately, especially early in the game, but they do present an interesting challenge.
Another thing to note is that the score prediction part involves using a rectifier to correct cases in the chase that may not make sense to the viewer by considering what the win probability is in those situations. For example, if there is only a 40% chance of winning, the team’s projected score should not be higher than the target or if there is a 60% chance of winning, it should not be lower than what they are chasing.
def rectify_scores(results, win_prob_feature = 'pred_winner', score_feature = 'pred_score'):
temp = results.copy()
incorrect_pred = temp[(temp.innings == 2) & (temp[win_prob_feature] < 0.5) & (temp[score_feature] >= temp.target)]
temp.loc[incorrect_pred.index, score_feature] = incorrect_pred.target - 2
incorrect_pred = temp[(temp.innings == 2) & (temp[win_prob_feature] == 0.5)]
temp.loc[incorrect_pred.index, score_feature] = incorrect_pred.target - 1
incorrect_pred = temp[(temp.innings == 2) & (temp[win_prob_feature] > 0.5)]
temp.loc[incorrect_pred.index, score_feature] = incorrect_pred.target
return temp
These mostly occur when the probabilities are close to 50% and that is why a manual fix is necessary because it is difficult for the model to precisely determine the relationship between the two outputs. Ideally, however, it should be able to somehow do this on its own.
The full code for this project can be found here.